
以数据文件“马克威通用数据1.mkw”为例,演示决策树算法的操作。首先,在工作区内,打开建模分析工作流:“机器学习”→“决策树”,接着选择模型的训练或应用,然后选择数据源,并设置算法参数,最后双击运行按钮。具体的操作如下:
(1)模型训练
首先输入目标变量“目标变量”,响应变量为“变量1”、“变量2”、“变量3”、“变量4”、“变量5”、“变量6”,剪枝方法为“不剪枝”,将变量类型设置为“整型”,树生产方法为“信息熵”,输入变量如下所示,并选择保存模型的路径,设置如下图所示:
 决策树-属性设置
决策树-属性设置
选项说明
生成树方法:选择成树的判别标准:
信息熵:选择此项,系统将在树的每个节点上使用信息熵度量选择测试属性。具体做法是:选择具有最大信息熵的属性作为当前节点的测试属性。使用该法的前提是所有属性都是分类的,即取离散值,连续值的属性必须离散化。
GINI系数:选择此项,系统将根据层间的GINI系数差来选择测试属性以及控制树的深度。具体的做法是:选择层间的最大GINI系数差所对应的属性作为当前节点的测试属性,当GINI差小于指定的标准时,停止树的增长。
树生成的限制:对决策树大小的控制:分裂时一个分支的最小样本:指定叶节点的最小实例数。连续值分叉接点的最大分叉:在此处设置将连续变量离散化为几类,默认值为3类。
树剪枝的方法:选择决策树的剪枝方法:
不剪枝:选择此项,即对决策树不进行剪枝。
先剪枝:即在下设条件得到满足之前就停止继续扩展决策树:
当信息增益小于__时停止增长:在生成树方法中选择信息熵时,此选项有效,默认值为0.06。
GINI差小于__时停止增长:在生成树方法中选择GINI系数时,此选项有效,默认值为0.15。
当树的深度大于__时停止增长:在生成树方法中选择信息熵或GINI系数时,此选项均有效,默认值为3。
后剪枝:
当错误率小于__ % 时允许剪枝:即错误率低于指定标准时,则开始剪枝,默认值0.3。
决策树运行结果树如下图:
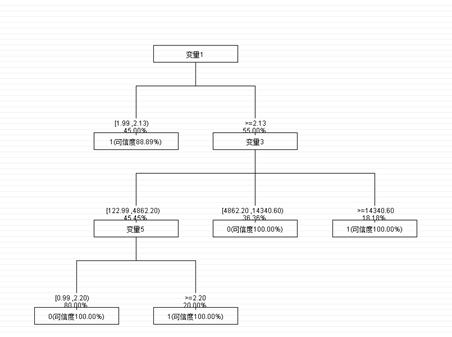 决策树-决策树
决策树-决策树
结果说明
从决策树图中可以看出,由顶到底可以有许多通路,每一个分枝路径都是一个规则。
(2)模型应用
完成模型训练后,可以应用模型对数据进行预测分析,选择“模型应用”标签,并选择模型来源,将模型变量与数据变量进行匹配,如下图:
 决策树-属性设置
决策树-属性设置
选项说明
模型来源:选择训练得到的模型,以进行预测应用。
变量设置:匹配模型中的变量和数据源中的变量。当加载模型文件后,系统会自动根据数据文件和模型文件进行同名匹配。用户也可以根据实际的需要,自定义匹配变量。
通过运行预测过程,得到结果如下:
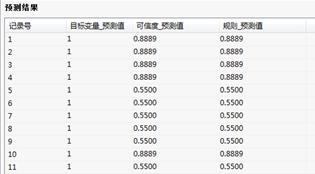 决策树-预测结果
决策树-预测结果
输入变量类型:整型、字符型。
决策树是一种基本的分类与回归方法。决策树分类器具有很好的准确性,已被成功的应用于许多的应用领域的分类,如医学、制造和生产、金融分析、天文学与分子生物学等;具体的包括欺诈监测、针对销售、性能预测、制造和医疗整段。决策树是许多商业规则归纳系统的基础。
决策树(Decision Tree)是应用于分类的一种树结构。其中的每个内部节点(internal node)代表对某个属性的一次测试判别,一个分枝代表一个测试结果,叶子(leaf)代表某个类(class)或者类的分布(class distribution)。最顶层的节点是根结点。可以将决策树理解为一个if-then规则的集合,由决策树的根节点到叶节点的每一条路径构建一条规则。
 决策树
决策树
决策树学习算法包含特征选择、决策树的生成和决策树的修剪过程,构造决策树的方法是采用自上而下的递归构造。
构造的思路是,如果训练样本集合中的所有样本是同类的,则将之作为叶子节点,节点内容即是该类别标记。否则,根据某种策略(如信息熵或GINI系数)选择一个属性,按照属性的各个取值,把样本集合划分为若干子集合,使得每个子集上的所有样本在该属性上具有同样的属性值,然后再依次递归处理各个子集。这种思路实际上就是“分而治之”的道理。
信息增益算法:
设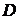 是
是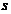 个样本的集合,具有
个样本的集合,具有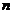 个不同的类别
个不同的类别 。设
。设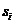 是类
是类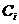 的样本数,那么对给定的样本分类所需要的经验熵为:
的样本数,那么对给定的样本分类所需要的经验熵为:
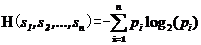
其中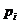 为任意样本属于类
为任意样本属于类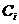 的概率,并用
的概率,并用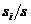 估计。
估计。
设属性 具有
具有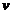 个不同的值
个不同的值 ,可以用属性
,可以用属性 将集合
将集合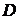 划分为
划分为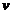 个子集
个子集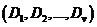 ,其中
,其中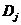 包含
包含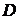 中属性
中属性 上取值
上取值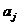 的一些样本。令
的一些样本。令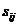 是子集
是子集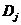 中类
中类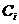 的样本数。根据
的样本数。根据 划分成子集的经验熵为:
划分成子集的经验熵为:
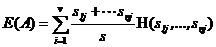
当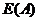 熵值越小,子集划分的纯度越高。
熵值越小,子集划分的纯度越高。
在属性A上分枝将获得的信息增益为:

通过比较每个特征的信息增益值,并比较它们的大小,选择信息增益最大的特征。
输出结果:
决策树结果信息:决策树的正确率。
决策树分类重要性:列出了决策变量的重要性。
决策树规则描述:列出不同规则的决策结果的可信度。
预测结果:列出记录的分类的预测值。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1366****031 | 2023-12-06 13:35:19 | 1年 | Windows | 单机版 |
| 1868****285 | 2023-08-17 13:31:11 | 1年 | Windows | 单机版 |
| 1786****815 | 2023-03-10 14:12:48 | 1年 | Windows | 单机版 |
| 1302****100 | 2020-06-16 13:15:32 | 1年 | Windows | 单机版 |
| 1801****427 | 2019-02-18 19:07:33 | 1年 | Windows | 单机版 |
| 1381****637 | 2019-01-10 20:29:13 | 1年 | Windows | 单机版 |
| 1884****551 | 2018-09-17 11:11:31 | 1年 | Windows | 单机版 |
| 1589****808 | 2018-09-09 00:55:29 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:13:07 | 1年 | Windows | 单机版 |
| 1832****368 | 2018-07-23 11:04:33 | 1年 | Windows | 单机版 |