
以数据文件“马克威通用数据3.mkw”为例,演示曲线回归算法的操作说明。该数据包含某试验要研究X条件对Y的影响,经过试验观察得到X、Y的6组记录值,试分析它们之间的非线性关系,定义变量X与Y。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“回归分析”→“曲线回归”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)其中各类参数的含义为:
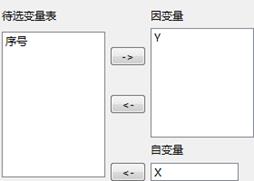
因变量:选入曲线拟合中的因变量。
自变量:可选择任意一个普通自变量,也可以选择时间作为自变量。
模型选择:用来选择所用的曲线拟合模型。
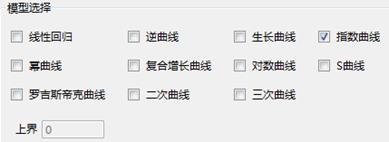
参数设置如下所示,自变量选择Y,因变量选择X,模型选择为“指数曲线”。
(5)输出结果:
模型分析:
回归系数分析:
拟合图:
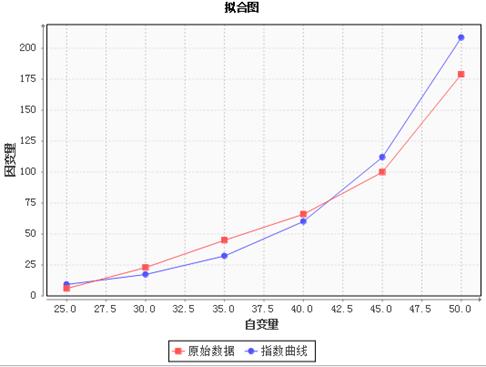
(6)结果说明:
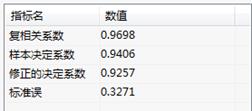
在模型分析表中给出了复相关系数、相关系数的平方、修正相关系数平方、标准误差四个指标;
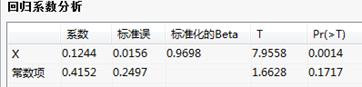
回归系数分析表给出在95%的置信水平下,自变量X对因变量Y的影响;
拟合图反映回归的拟合结果的情况,其中红色曲线代表原始数据,蓝色曲线代表拟和的指数曲线。
输入变量类型:整型、浮点型
(注:自变量可为一个或多个,但因变量只能一个)
输入数据尺度:标量型
曲线回归是对变量之间的非线性关系进行分析,应用曲线来拟合。通过适当的变换,将曲线模型转化为线性模型。可以确定两个变量间数量变化的某种特定的规则或规律;表示曲线特点的参数:如回归参数、极大值、极小值和渐近值等。
线性回归不能解决所有问题,对有的问题可以通过函数的转换,在一定范围内将因变量和自变量的关系变为线性关系;但这种转换可能导致更复杂的计算或者失真;所以可以用曲线拟合的方法,建立简单且合适的模型。
曲线回归的第一步骤是将数据简单的绘制在图形上,并观察数据的分布情况以便确定所应采取的模型。利用曲线估计可以方便地进行线性拟合、增长曲线拟合、指数拟合、对数拟合等。
系统提供了多种曲线拟合的模型,包括线性回归、逆曲线、生长曲线、指数曲线、幂回归、复合增长曲线、对数曲线、S曲线、罗吉斯蒂克曲线、二次曲线和三次曲线。最终采用哪种拟合模型则主要取决于模型能否对数据作充分描述。
输出结果:
模型分析表:给出了复相关系数、样本决定系数、修正的决定系数、标准误四个指标,它们是反映模型拟合优劣的指标。复相关系数接近 1,说明模型拟合程度较好。
方差分析表:给出模型中自变量对因变量变异的影响,显著性小于0.05,模型中自变量对因变量产生的影响较大。
回归系数分析表:给出在95%的置信水平下,自变量及常数项对因变量的影响,概率检验值小于0.05,拒绝零假设,影响显著。
拟合图:反映回归的结果情况。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1355****728 | 2022-03-24 10:52:53 | 1年 | Windows | 单机版 |
| 1371****011 | 2020-09-30 21:22:13 | 1年 | Windows | 单机版 |
| 1590****631 | 2020-07-09 12:57:44 | 1年 | Windows | 单机版 |
| 1305****178 | 2019-12-27 18:05:32 | 1年 | Windows | 单机版 |
| 1305****178 | 2019-12-27 18:05:32 | 1年 | Windows | 单机版 |
| 1886****092 | 2018-09-02 10:13:17 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:52:02 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1505****848 | 2018-04-25 08:43:30 | 1年 | Windows | 单机版 |
| 1505****848 | 2018-04-22 21:50:51 | 1年 | Windows | 单机版 |