
以数据文件“马克威通用数据2.mkw”为例,演示指数平滑模型算法的操作。在进行指数平滑模型分析前,可以利用统计图形,对序列的走势、周期或平稳性做出一个大致的判断,以便对模型的参数设置有一个比较正确的最初判断,把握分析的方向。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“时间序列”→“指数平滑模型”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要操作步骤如下:
1)选择数据源;
2)参数设置:
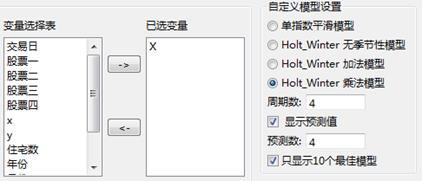
自定义模型设置:选择平滑拟合的模型。
周期数:可选择4~12之间的任意整数。一般选择4或12,若选择4,则分析季度对序列的影响;选择12,则分析月度对序列的影响。
显示预测值:用于选择是否产生预测值。若选中该项时,则需要设置预算数,如5,则系统将给出所分析的序列的向后5个预测值。
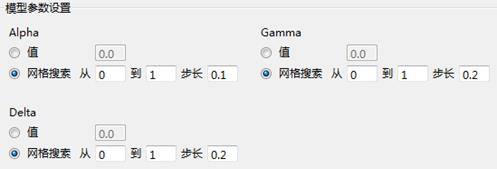
模型参数设置:
平滑系数:Alpha越大说明近期的影响越明显,Alpha越小说明序列变化越稳定,不易受近期随机变动的影响。Alpha适用于各个模型。
线性回归系数:Gamma适用于线性趋势和指数趋势模型,不适用于有季节成分或无趋势的模型。
季节因子:Delta适用于所有有季节成分的指数趋势模型,不适用于线性趋势或无趋势的模型。
由用户指定相应的参数值。Alpha、Gamma、Delta的取值范围是[0,1]。
网络搜索:即遍历法搜索,系统让相应的模型参数从0到1,每次增加一个步长来估计预测的模型。系统将根据各个模型的残差平方和(SSE)来对模型进行评判,选取其中SSE最小,即最优的参数组合(模型)建立指数平滑。
只显示10个最佳模型:指定输出拟合模型(拟合序列)的个数,网络搜索模型参数时有效。在进行网络搜索时,系统会对各参数的不同取值排列组合拟合模型,如果选择该项,则在结果窗口中只显示残差平方和(SSE)最小的10个拟合模型,不选择该项,将输出所有可能的拟合模型。
参数设置如下所示,本案例选取数据集字段“X”作为分析对象:
(5)输出结果:
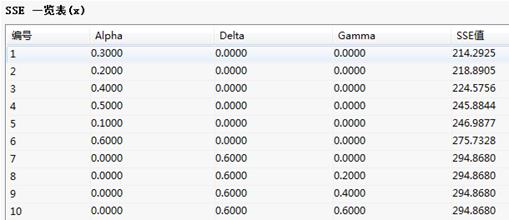
SSE一览表:
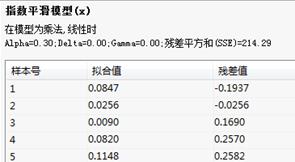
指数平滑乘法模型:
(6)结果说明:
本例中系统将根据这三个参数进行网格扫描生成指数平滑模型,在“SSE一览表”中列出10个最佳模型的SSE值,并给出最优模型的拟合序列值和残差值。
输入变量类型:整型、浮点型
(注:输入数据可分为周期性和非周期性两种:具有周期性质的序列以及相应的年、月,非周期性数据t>=1即可。两者都不处理数据有缺失情况。)
输入数据尺度:标量型、有序型
指数平滑是进行趋势分析和预测时常用的一种方法,适用于拟合与预测没有明显趋势和季节波动的序列。
指数平滑它是利用修匀技术,削弱短期随机波动对序列的影响,使序列平滑化,从而显示出长期趋势变化的规律。用序列过去值的加权均值来预测将来的值,序列中近期的数据被赋以较大的权重,远期的数据被赋以较小的权重。理由是一般情况下,某一变量值对其后继行为的影响作用是逐渐衰减的。
系统提供四种指数平滑的模型备用户选择:单指数平滑模型、Holt_Winter无季节性模型、Holt_Winter加法模型、Holt_Winter乘法模型。
单指数平滑模型,即一次指数平滑,表达式及预测公式为:
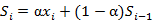 ,
,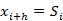
无季节模型,即二次指数平滑,表达式及预测公式为:
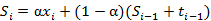
 ,
,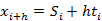
加法模型,即三次指数平滑累加,表达式及预测公式为:
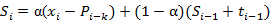

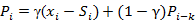 ,
,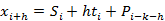
乘法模型,即三次指数平滑累乘,表达式及预测公式为:
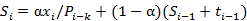

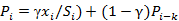 ,
,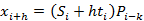
其中参数 的值都位于[0,1]之间,可多实验几次已达到最佳效果;同时
的值都位于[0,1]之间,可多实验几次已达到最佳效果;同时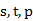 的初始值选取对于算法整体影响不是特别大,通常取值为:
的初始值选取对于算法整体影响不是特别大,通常取值为: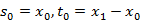 ,加法模型P=0,乘法模型P=1。
,加法模型P=0,乘法模型P=1。
输出结果:
SSE一览表:列出10个最佳模型的残差平方和SSE值
指数平滑模型:给出最优模型的拟合序列值和残差值
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1828****691 | 2024-03-04 16:47:45 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:14:11 | 1年 | Windows | 单机版 |
| 1763****680 | 2018-06-24 15:58:48 | 1年 | Windows | 单机版 |
| 1505****848 | 2018-04-25 08:43:30 | 1年 | Windows | 单机版 |
| 1505****848 | 2018-04-22 21:48:39 | 1年 | Windows | 单机版 |
| 1505****848 | 2018-04-22 21:48:11 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1825****295 | 2017-10-13 09:29:23 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1581****857 | 2017-06-20 07:47:54 | 1年 | Windows | 单机版 |