
以数据文件“马克威通用数据3.mkv”为例,演示偏最小二乘回归模型;此例中的具体变量含义如下:
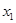 : 直接蒸馏成分;
: 直接蒸馏成分;
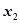 : 重整汽油;
: 重整汽油;
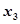 : 原油热裂化油
: 原油热裂化油
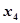 : 原油催化裂化油;
: 原油催化裂化油;
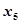 : 聚合物;
: 聚合物;
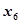 : 烷基化物
: 烷基化物
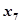 : 天然香精;
: 天然香精;
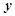 :原辛烷值
:原辛烷值
自变量为: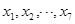 ,因变量为
,因变量为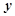 ;在实际生产过程中,这7个自变量之间存在关系:
;在实际生产过程中,这7个自变量之间存在关系:
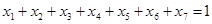
(1)首先,在工作区,打开建模分析工作流选择“高级统计”→“偏最小二乘法”→“偏最小二乘回归模型”;
(2)接着选入数据源;
(3)然后设置算法的参数;
(4)具体操作步骤如下:
1)选择数据源;
2)变量选择:
待选变量列表:列出数据源中所有的变量;
自变量:回归分析中的解释变量,可以同时选择多个;
因变量:回归分析中的被解释变量,也可以同时选择多个;
主成分个数:主成分个数的提取方法;
交叉验证:根据交叉验证原理,系统自动提取主成分个数
模型的拟合度:提取的主成分个数按照主成分对因变量的拟合度来确定,使得主成分对因变量的拟合度大于指定的拟合度 。
用户指定:主成分个数为用户指定的个数,一般指定的值必须为正整数。
最大迭代次数和迭代精度:在求主成分的过程中,如果迭代次数超过
指定次数或者达到了指定精度,则迭代结束;
交叉验证分组:把所有样本点分成两部分:第一部分除去某个样本点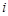 的所有样本点集合(共含
的所有样本点集合(共含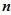 -1个样本点),用这部分样本点并使用h个成分拟合一个回归方程;第二部分是把刚才被排除的样本点
-1个样本点),用这部分样本点并使用h个成分拟合一个回归方程;第二部分是把刚才被排除的样本点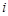 代入前面拟合的回归方程,得到
代入前面拟合的回归方程,得到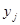 在样本点
在样本点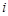 上的拟合值
上的拟合值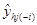 。
。
设置好参数如下所示:
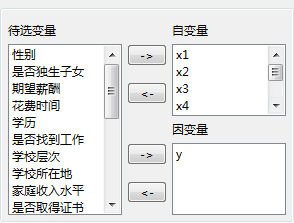
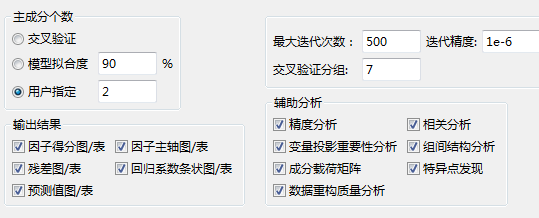
(5)输出结果:
相关系数矩阵表:
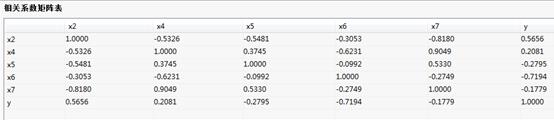
预测误差平方和:
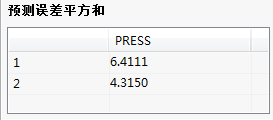
拟合度以及交叉有效性表:
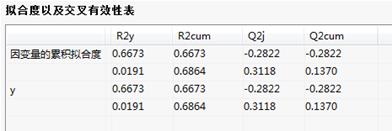
回归系数表:
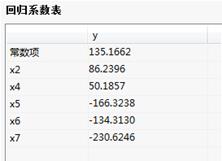
自变量、因变量因子得分表:
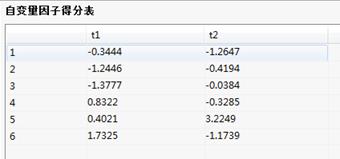
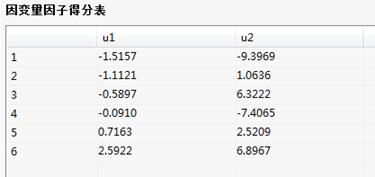
自变量主轴:
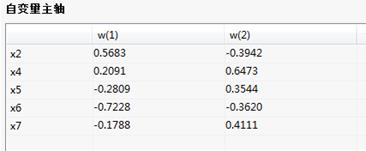
因变量主轴:
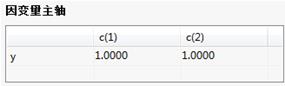
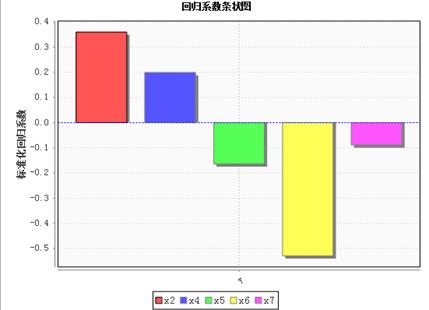
回归系数条状图:
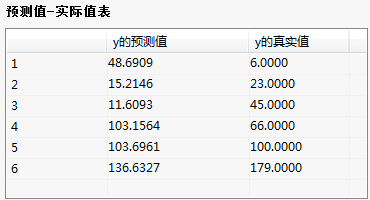
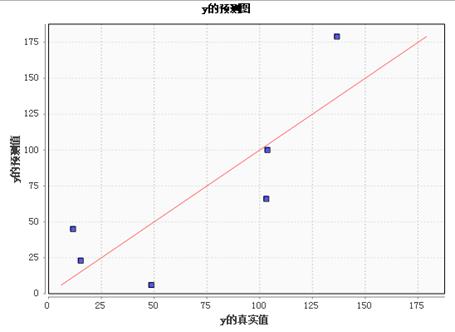
实际值与预测值、拟合图:
(6)结果说明:
相关系数矩阵表:各个变量之间的相关性
交叉拟合度:可以看出根据交叉有效性的判断
回归系数条状图:自变量 ,
,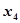 对因变量
对因变量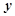 为正向的影响关系,而自变量
为正向的影响关系,而自变量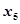 ,
,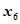 ,
,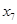 对因变量
对因变量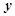 为负向的影响关系。
为负向的影响关系。
实际值与预测值表、拟合图:预测值以及实际值表,并在二维坐标系中表现出来。
输入变量类型:整型、浮点型,数据要求没有缺损。
输入数据尺度:标量型
偏最小二乘回归是一种新型的多元统计数据分析方法;是一种多因变量对多自变量的回归建模方法。可以较好地解决许多以往用普通多元回归无法解决的问题,可以实现多种数据分析方法的综合应用。
偏最小二乘回归可应用在:自变量存在严重多重相关性的条件下进行回归建模、允许在样本点个数少于变量个数的条件下进行回归建模。
由于自变量之间会存在大量的自相关情况,所以对这类问题使用普通的最小二乘法不能够求解;这是因为变量多重相关性会严重危害参数估计,扩大模型误差,并且破坏模型的稳定性。偏最小二乘法开辟了一种有效的技术途径,它利用对系统中的数据信息进行分解和筛选的方式,提取对因变量的解释性最强的综合变量,辨识系统中的信息与噪声,从而更好地克服变量多重相关性在系统建模中的不良作用。
下面给出偏最小二乘法的标准算法:
第一步:对原始数据X和Y进行中心化得到X0和Y0,并从Y0中选择方差最大的一列作为u1,方便后面计算方便;
第二步:迭代求解X与Y的变换权重(w1,c1)和因子(u1,t1),直到收敛;
计算公式:
利用第一步选择的Y中的列,求解X的变换权重因子
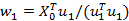 ,
, 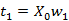
利用X的信息t1,求解Y的变换权重c1,并且更新因子u1的值
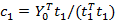 ,
, 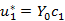
判断是否已找到合理的解,否则继续寻找。
第三步:求X与Y的残差矩阵;
计算公式:
1)求X的载荷P1,载荷是反映X0和因子T1的直接关系;
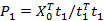
2)求X0的残差X1,残差表示了u1不能反映X0信息的部分;
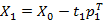
3)求Y的载荷Q1;
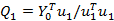
4)建立X因子t1与Y因子u1之间的回归模型,并用t1预测u1的信息;
 ,
,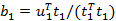
5)求Y0的残差Y1,这个值表达了X与因子t1所不能预测的Y0中的信息;
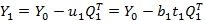
第四步:利用X1与Y1,重复上述步骤,求解下一批偏最小二乘的参数。
输出结果:
回归系数图:在回归系数图表中给出了原始数据的自变量对因变量的表示形式以及标准化数据的自变量对因变量的表示系数;
因子得分图/表:在计算过程中所得到的主成分的值以及相应的序列图;因子得分是通过降维的方法找到的可以显著的代表原始变量的成分。因子得分值有两种,一种为自变量因子得分,一种为因变量因子得分;
因子主轴图/表:给出因子的值和图;
预测值图:给出了因变量的预测值;
残差图:实际值与预测值之间的差异;
辅助分析:精度分析、相关分析、变量投影的重要性指标、成分载荷矩阵、组间结构分析、特异点分析和数据重构质量分析。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1883****167 | 2022-11-29 10:38:07 | 1年 | Windows | 单机版 |
| 1398****386 | 2021-06-18 20:37:14 | 1年 | Windows | 单机版 |
| 1530****827 | 2019-05-28 21:43:01 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:46:24 | 1年 | Windows | 单机版 |
| 1502****642 | 2018-07-23 09:56:13 | 1年 | Windows | 单机版 |
| 1864****834 | 2018-03-28 16:47:56 | 1年 | Windows | 单机版 |
| 1552****636 | 2018-03-19 16:44:56 | 1年 | Windows | 单机版 |
| 1552****636 | 2018-03-19 16:42:46 | 1年 | Windows | 单机版 |
| 1362****882 | 2018-01-27 11:49:16 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |