
以数据文件“马克威通用数据1.mkw”为例,演示粗糙集算法的操作,利用粗糙集理论对决策表进行约简。首先,在工作区内,打开建模分析工作流:“机器学习”→“粗糙集”,接着选择数据源,然后设置算法参数,最后双击运行按钮。把示例中“mileage”为决策属性,“size”为指定条件属性,“number_of_cylinders”、“presence_of_a_turbocharger”、“type_of_fuel_system”、“engine_displacement”、“compression_ratio”、“power”、“type_of_transmission”、“weight”,其他变量为一般条件属性,设置参数后如下所示:
 粗糙集-属性设置
粗糙集-属性设置
选项说明
决策属性:选择决策表中的决策属性,只能选一个。
一般条件属性:选择决策表中的条件属性。
指定条件属性:指定要保留的属性,即该属性不论计算结果如何,进行属性约简时不能够删除它,但提取规则时可能会忽略它。
运行得到的结果如下:
 粗糙集-树形结果列表
粗糙集-树形结果列表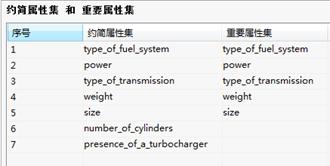 粗糙集-重要属性集
粗糙集-重要属性集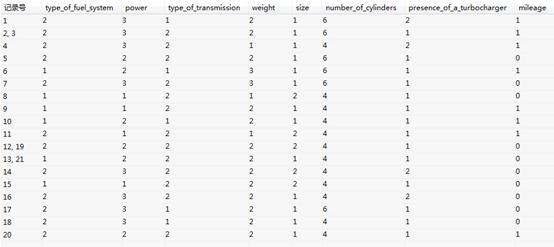 粗糙集-约简属性集
粗糙集-约简属性集 粗糙集-决策规则表
粗糙集-决策规则表
输入变量类型:数值型。(注:输入变量的数据必须为离散型数据,连续性数据必须先离散化)
粗糙集理论能够提供有效的技术用于数据挖掘的数据预处理、数据缩减、规则生成、数据依赖关系发现等方面,故该理论目前作为数据挖掘领域的一种主流方法,也正受到越来越多研究者的关注,并开始被广泛应用于数据挖掘、机器学习、决策支持系统和模式识别等众多领域。粗糙集主要用于特征归约,能识别和删除无助于给定训练数据分类的属性,提炼出重要属性和约简属性集。
粗集(rough sets,RS)理论是80年代初由波兰科学家Pawlak提出的一种处理模糊性和不确定性的数学工具。它从一个新的角度将知识定义为对论域的划分能力,并将其引入数学中的等价关系来进行讨论,从而为数据分析,特别是不精确、不完整数据分析提供了一套新的数学方法。
粗糙集理论是一种新的处理模糊和不确定性知识的数学工具。其主要思想是在保持分类能力不变的前提下,通过知识约简,导出问题的决策或分类规则。粗糙集分析方法中用到的数据类型为离散型数据,对于连续型数据必须在处理前离散化。
基本概念
定义1 一个信息系统是一个四元组,可表示为:
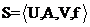
其中 为对象的非空有限集合;
为对象的非空有限集合;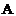 为属性的非空有限集合;
为属性的非空有限集合;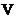 为属性的值域集;
为属性的值域集;  为信息函数,
为信息函数,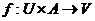 。如果
。如果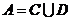 ,
,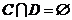 ,
,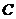 为条件属性集,
为条件属性集, 为决策属性集,则把信息系统
为决策属性集,则把信息系统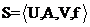 称为决策系统,用
称为决策系统,用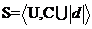 或
或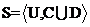 来表示,其中
来表示,其中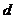 为单一的决策属性。从数据库的角度来看,决策系统就是一张表,其中
为单一的决策属性。从数据库的角度来看,决策系统就是一张表,其中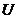 是记录集合,
是记录集合,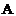 是字段集合,每一个对象对应一条记录,这样决策系统又可称为决策表。
是字段集合,每一个对象对应一条记录,这样决策系统又可称为决策表。
定义2 在决策系统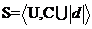 中,对于
中,对于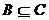 ,则B在U上的不可分辨关系定义为:
,则B在U上的不可分辨关系定义为: ,
,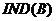 把
把 划分为
划分为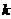 个等价类,
个等价类,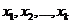 ,
,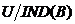 表示等价关系
表示等价关系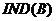 的所有等价类组成的等价类族,即有:
的所有等价类组成的等价类族,即有: ![]() 。
。
定义3 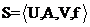 ,分类价
,分类价 关于条件属性
关于条件属性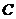 的正域(简称
的正域(简称 的
的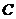 正域)定义为:
正域)定义为:
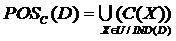
其中,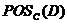 包含了
包含了 中所有能被
中所有能被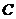 正确分类为
正确分类为 中一类的对象。
中一类的对象。 在
在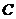 上的依赖度定义为:
上的依赖度定义为:
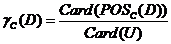
—个属性 ,如果
,如果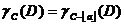 ,则
,则 称为为可去除的;否则称为不可去除的。
称为为可去除的;否则称为不可去除的。
属性集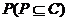 称为
称为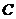 的一个约简,如果满足以下条件:
的一个约简,如果满足以下条件:
 ,
,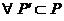
一个条件属性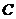 的约简是具有同
的约简是具有同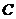 相同分类能力的一个
相同分类能力的一个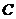 的子集,并且约简中的任意一个属性都不能在不降低其分类能力的前提下被删除。
的子集,并且约简中的任意一个属性都不能在不降低其分类能力的前提下被删除。
输出结果:
重要属性集:列出决策表中的核值。
约简属性集:列出决策表中的核值和用户指定属性。
约简表:列出决策表中的核值、用户指定属性和对应的决策属性
决策规则:列出记录的分类结果。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1357****252 | 2024-01-11 15:46:58 | 1年 | Windows | 单机版 |
| 1583****651 | 2023-09-10 20:53:30 | 1年 | Windows | 单机版 |
| 1583****651 | 2023-09-10 20:52:53 | 1年 | Windows | 单机版 |
| 1786****815 | 2023-03-10 14:12:48 | 1年 | Windows | 单机版 |
| 1530****827 | 2019-08-27 16:14:15 | 1年 | Windows | 单机版 |
| 1875****696 | 2019-03-05 17:04:19 | 1年 | Windows | 单机版 |
| 1801****427 | 2019-02-18 19:07:33 | 1年 | Windows | 单机版 |
| 1563****680 | 2018-08-21 13:41:16 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:13:07 | 1年 | Windows | 单机版 |
| 1580****630 | 2018-07-17 10:05:56 | 1年 | Windows | 单机版 |