
警报分析:某水文站内装有一个小型的警报系统,与该警报是否拉响相关的因素有:洪水到来、地震发生。同时该系统还肩负着安全警报的功能:当水文站发生入室盗窃时,警报同样也会拉响。而洪水的到来与降雨情况有关,地震的发生会反映在地震监测仪的报告中。同时,入室盗窃也会带来地震监测仪的扰动。在水文站以往的数据库中,关于以上这些因素都能找到详细的记录。我们可以用下图所示的网络结构来描述这些因素之间的因果关系:
 贝叶斯网络实例
贝叶斯网络实例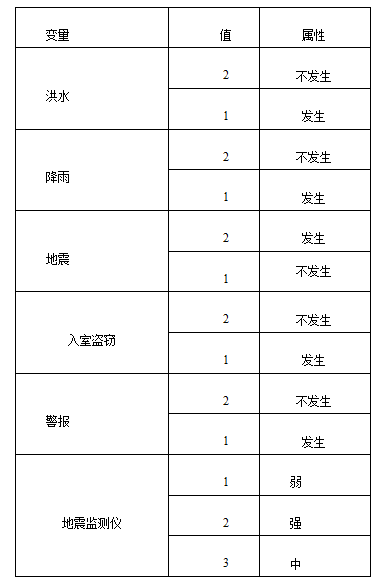
首先,在工作区内,打开建模分析工作流:“机器学习”→“贝叶斯网络”,然后选择数据来源,下面将按步骤说明建立上述贝叶斯网络进行推理分析的过程。
(1)新建网络推理
对于初次建立的网络,数据选择为“马克威通用数据1.mkw”,在模型任务栏选择“新建网络推理”,分析字段为“洪水”、“降雨”、“地震检测仪”、“警报”、“地震”、“入室盗窃”,将无用的节点删除。首先对节点进行编辑,节点名称取“洪水”“降雨”、“地震检测仪”、“警报”、“地震”、“入室盗窃”。
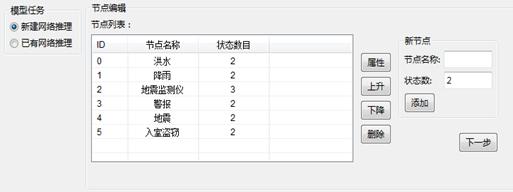 贝叶斯网络-节点编辑
贝叶斯网络-节点编辑
节点列表:显示数据文件中的节点(变量),状态数目即为变量中不同值的个数。
上升:将选中的节点上移一个位次。
下降:将选中的节点下移一个位次。
删除:删除选中的节点。
添加:添加新的状态节点,要求设置新节点的名称和状态数。其中状态数必须是大于1的自然数,且不允许新的节点与列表中已有的节点发生重名。
属性:打开节点属性编辑界面(如下图所示),可编辑选中节点的属性。
 贝叶斯网络-节点属性编辑
贝叶斯网络-节点属性编辑
选项说明
修改节点名称:在文本框里修改当前节点的名称。
删除状态:删除选中的状态值。
修改状态:将选中的状态值修改为文本框中输入的新值。
添加状态:添加文本框中的值为当前变量的新状态值。
确定:修改完成,确认执行当前修改,并返回节点编辑界面。
取消:取消执行节点属性修改,并返回节点编辑界面。
关系编辑
对于当前的数据,可以跳过节点属性编辑的过程。点击“下一步”进入到关系编辑的界面。在关系编辑的界面,根据各节点之间的因果关系设置关系网络如下:
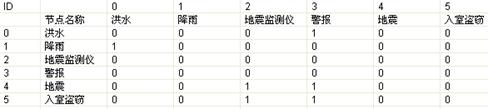 贝叶斯网络-关系编辑
贝叶斯网络-关系编辑
节点关系编辑界面用来设定节点之间的因果联系,用表格的形式来表示。表格的行数和列数均等于节点的总个数,其中:行表示原因节点,即箭头出发的节点;列表示结果节点,即箭头到达的节点。
矩阵元素有0和1两种,0表示从该行所对应的节点到该列所对应的节点之间不存在因果关系,1则表示从该行所对应的节点到该列所对应的节点之间存在因果关系,且该行所对应的节点为原因,该列所对应的节点为结果。
表格初始状态元素全为0,当鼠标双击某个单元格时,其中的元素会从0变为1,或从1变为0,但对角元素始终为0,不会发生改变。重置按钮可清除节点关系表的全部设置,返回初始状态。
保存模型后,继续点击“下一步”,系统弹出贝叶斯网络的构建成果。
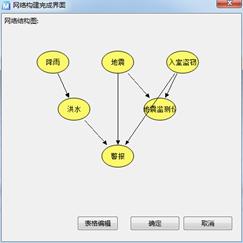 贝叶斯网络-网络结构图
贝叶斯网络-网络结构图
点击“表格编辑”查看概率表:
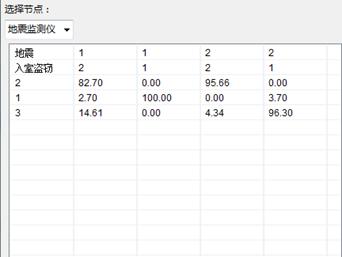 贝叶斯网络-概率表
贝叶斯网络-概率表
选项说明
选择节点:选择要查看的节点以查看对应的概率表。在概率表中,每一行对应当前节点每一个状态取值,每一列对应该节点的父节点的一个状态(当父节点多于一个时,对应父节点的一个状态组合)。表格中每i行j列的元素即为在父节点处于第j列状态下,本节点取第i行状态值的概率,即所谓的条件概率。因此,表格中每一列的概率之和都等于1。对于没有父节点的节点(即根节点),其概率表仅由一列构成,称作边缘概率表。概率表也称为网络参数。
编辑表格:在概率表中,用户根据手头的统计数据或自身的经验知识、领域内的专家知识调整每个节点的概率表。针对用户修改后,概率之和不等于1的列,系统会在点击“应用”或“确定”按钮后自动进行归一化计算。点击“确定”执行对概率表的修改。
确认各概率表和网络结构后,点击确定返回系统主界面,并进入到推理过程。
此处假设某时刻警报突然拉响了,且此时正在下雨,值班人员要判断此时发生地震、盗窃和洪水的概率分别是多少,以便采取相应的措施加以应对,可以借助贝叶斯网络推理来支持决策。
在推理设置中,选择降雨和警报为已知节点,并设置两者观察值为1(即发生),再选择洪水、地震和入室盗窃为未知节点,要求进行10,000次蒙特卡洛采样,如下图:
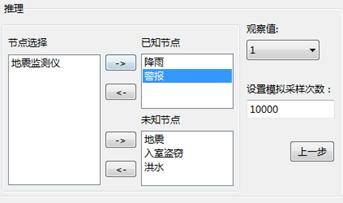 贝叶斯网络-属性设置
贝叶斯网络-属性设置
选项说明
已知节点:选择已知节点,并指定已知观察值。
未知节点:设置未知节点,即推理的目标节点。
设置模拟采样次数:设置蒙特卡洛模拟采样次数。
双击“运行”节点启动运行,结果如下图所示:
 贝叶斯网络-树形结果列表
贝叶斯网络-树形结果列表
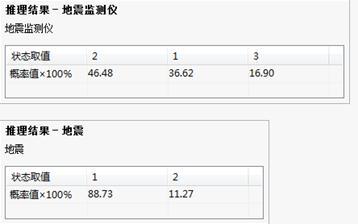 贝叶斯网络-推理结果
贝叶斯网络-推理结果 贝叶斯网络-概率柱状图
贝叶斯网络-概率柱状图
从结果中可以看到,贝叶斯网络推理结果认为警报很可能是发生洪水引起的。
(2)已有网络推理
通过学习来获取贝叶斯网络参数的过程,对于已建立了贝叶斯网络的推理(即通过参数设置推理过程),可以选择“已有网络推理”直接进入到推理过程。
加载模型文件后,点击“下一步”进入到推理参数设置界面。此处假设:在下雨天警报突然拉响,如果此时值班人员还注意到了地震监测仪的状态处于弱信号的范围,仍借助贝叶斯网络进行推理。
在推理设置中,选择降雨和警报为已知节点,并设置两者观察值为1(即发生),再选择地震监测仪为已知节点,观察值为1(即弱信号),同时选择洪水、地震和入室盗窃为未知节点,要求进行10,000次蒙特卡洛采样,如下图:
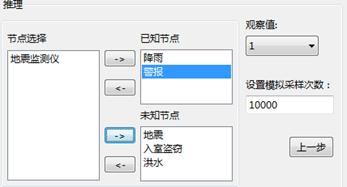 贝叶斯网络-属性设置
贝叶斯网络-属性设置
双击“运行”节点启动运行,结果如下图所示:
 贝叶斯网络-树形结果列表
贝叶斯网络-树形结果列表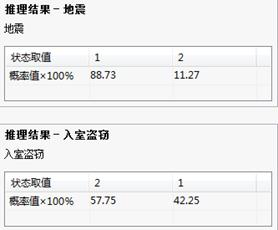
 贝叶斯网络-推理结果
贝叶斯网络-推理结果
从以上结果中可以看到,由于增加了地震监测仪信号为弱的初始条件,例2所得的地震发生的概率变得更小。该推理结果认为警报拉响最有可能是洪水引起的。
特征要求:变量之间满足一定的条件独立关系,且此条件独立关系能够用一个有向无环图来描述
输入变量类型:整数型。
贝叶斯网络适用于由离散变量构成的数据集合,变量之间满足一定的条件独立关系,且此条件独立关系能够用一个有向无环图来描述。贝叶斯网络可以针对给定的任务实现预测、分类、诊断、聚类、因果分析等数据挖掘的功能。根据初始条件和推理目标的不同,贝叶斯网络的应用类型各不相同。
基本原理
贝叶斯网络(Bayesian networks or Bayesnets)也称为因果概率网络(CPNs,Causal Probabilistic Networks)、贝叶斯信念网络(BNs,Bayesian belief Networks)或信念网络,是用来对那些带有不确定性问题的问题域进行建模的系统。
从形式上说,贝叶斯网络是由一组以单向箭头相连的节点以及与每个节点相对应的概率函数所构成的网络。对于离散变量的贝叶斯网络,概率函数便具有了概率表的形式。这个网络必须是一个有向无环图,即其中不存在一条起始和终止于同一节点的通路。用图形的方法描述数据间的相互(因果)关系,语义清晰、可理解性强,有助于利用数据间的因果关系进行诊断、预测、分类等分析。因而贝叶斯方法具有独特的不确定性知识表达形式、丰富的概率表达能力、综合先验知识的增量学习特性等优点。
在贝叶斯网络中,每个节点代表一个有限状态数的离散随机变量,节点之间的单向箭头代表其间的因果关系。如果某个节点不具有父节点(即没有箭头指向它),那么这个节点就具有一个边缘概率表,其中记录了该节点取不同状态值的概率分布;反之,若某节点有父节点(即存在一条或多条有向箭头指向它),则它就拥有一个条件概率表。条件概率表中的每个元素对应该节点在其父节点处于某种状态组合下,其本身状态值的概率分布规律。
贝叶斯网络根据每个节点的概率表,在给定部分(一个或多个)节点状态值的前提下,对其余全部或部分节点的概率分布进行预测的过程即为网络的推理过程。
分析流程
贝叶斯网络的分析流程通常由三个步骤组成,即1)网络建立,2)参数学习或参数设置,3)网络推理,如图所示。
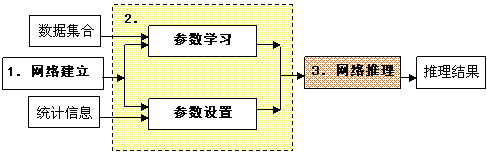 图 0-14 贝叶斯网络分析流程
图 0-14 贝叶斯网络分析流程
其中,具体原理如下:
1)网络建立:为一组具有潜在关系的变量建立起确定的因果关系的过程。这个过程需要提供领域专家根据各变量之间客观存在的因果关系以及其自身掌握的专家知识(即经验知识),对节点之间的因果联系给出一个确定的描述。并且保证其对应的图形要满足有向无环图的条件。
2)参数学习或设置:在网络结构建立的基础上,将实际的样本数据提供给网络学习算法,由此统计得到每个变量的状态值及个数,计算每个节点的参数(即概率表,包括边缘概率表和条件概率表)的过程被称为参数的学习过程。而参数设置是指在无法提供具体样本数据的情形下,只提供条件概率信息以设置必要的贝叶斯网络参数的过程。
3)网络推理:经过了网络建立和参数学习(或设置)的贝叶斯网络已经具备了进行推理的能力。针对每一次特定的推理任务,需要指定推理的初始条件,即指定当前已经观察到的变量及其所处的状态,。初始条件可以是多个变量及其状态所构成的集合。然后,贝叶斯网络将根据自身网络参数和推理初始条件进行蒙特卡洛模拟采样,当采样数量达到要求后,由推理算法计算出相应的推理结果。结果中包含每一个目标变量在其各状态值上的概率分布。
输出结果:
推理结果:列出推理的结果及概率。
概率柱状图:推理结果的概率柱状图。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1786****815 | 2023-03-10 14:12:48 | 1年 | Windows | 单机版 |
| 1521****939 | 2022-03-02 17:52:51 | 1年 | Windows | 单机版 |
| 1341****028 | 2022-01-27 15:34:25 | 1年 | Windows | 单机版 |
| 1341****028 | 2022-01-27 15:32:26 | 1年 | Windows | 单机版 |
| 1391****327 | 2020-09-28 20:40:56 | 1年 | Windows | 单机版 |
| 1506****206 | 2020-08-31 15:42:54 | 1年 | Windows | 单机版 |
| 1731****230 | 2020-08-04 10:44:43 | 1年 | Windows | 单机版 |
| 1535****704 | 2020-07-22 02:02:18 | 1年 | Windows | 单机版 |
| 1833****189 | 2020-07-14 16:58:13 | 1年 | Windows | 单机版 |
| 1880****695 | 2020-06-11 14:42:21 | 1年 | Windows | 单机版 |